Skip List Performance

C++ Performance Tests

The time performance tests are run as follows:

$ cd src/cpp
$ make release
$ ./SkipList_R.exe
                 test_very_simple_insert(): PASS
                                                    ...
                 test_roll_med_even_mean(): PASS
               perf_single_insert_remove(): 451.554 (ms) rate x.xe+06 /s
                                                    ...
            perf_roll_med_odd_index_wins(): vectors length:  1000000 window width: 524288 time: x.x (ms)
                            perf_size_of(): size_of(       1):      216 bytes ratio:      216 /sizeof(T):       x
                                                    ...
Final result: PASS
Exec time: x.x (s)
Bye, bye!

The ouptut is a combination of test results, performance results and dot visualisations

If multi-threaded support is enabled (see Multi-threaded C++ Performance below) the execution time including the multi-threaded tests takes about three minutes. With single threaded support the tests take around two minutes. If the debug version is built the performance tests are omitted as the cost of integrity checking at every step is very high which would make the performance test data irrelevant.

Time Performance

The performance test mostly work on a SkipList of type double that has 1 million values. Test on a couple of modern 64 bit OS’s [Linux, Mac OS X] show that the cost of SkipList operations is typically as follows.

Mutating operations: insert(), remove()

These operations depend on the size of the SkipList. For one containing 1 million doubles each operation is typically 450 ns (2.2 million operations per second).

Here is a graph showing the cost of the combined insert() plus remove() of a value in the middle of the list, both as time in (ns) and rate per second. The test function is perf_single_ins_rem_middle_vary_length().

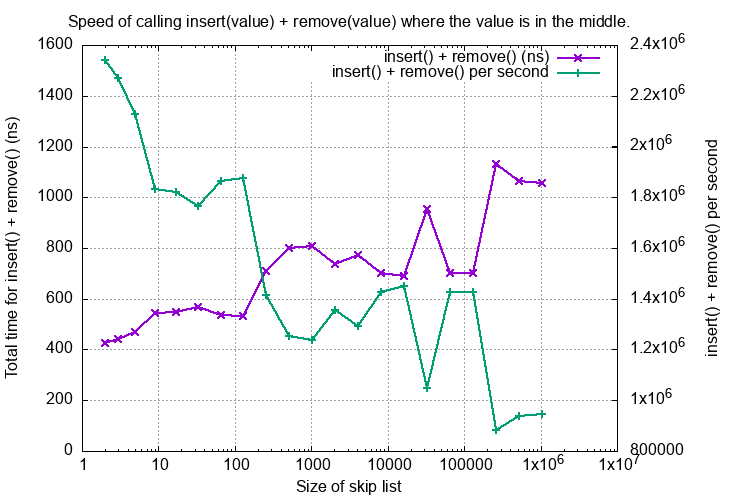
This shows good O(log(n)) behaviour where n is the SkipList size.

Indexing operations: at(), has() index()

These operations on a SkipList containing 1 million doubles is typically 220 ns (4.6 million operations per second).

vs Location

Here is plot of the time taken to execute at() or has() on a SkipList of 1 million doubles where the X-axis is the position in the SkipList of the found double. The test functions are respectively perf_at_in_one_million() and perf_has_in_one_million().

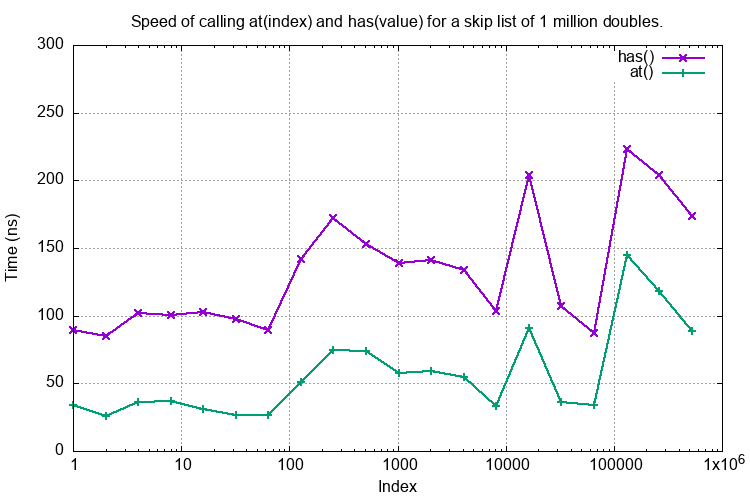
This shows fairly decent O(log(n))’ish type behaviour.

The index(value) method has similar behavour:

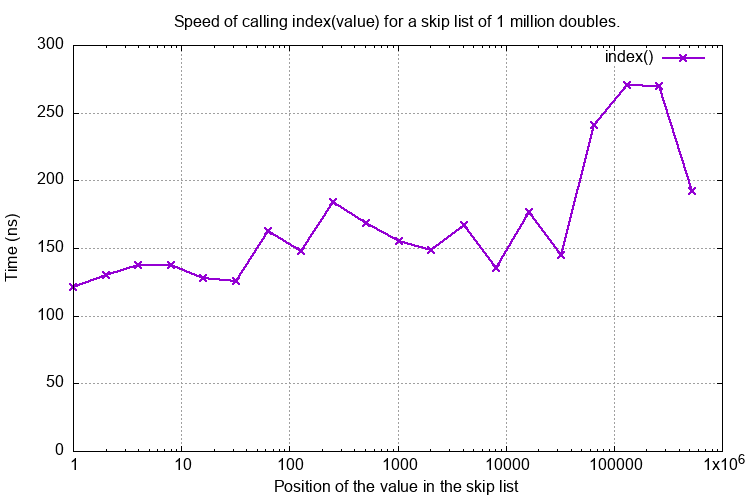
Rolling Median

Here is a plot of the time taken to compute a rolling median on one million values using different window sizes. The number of results is 1e6 - window size. This needs to insert(new_value) then at(middle) then remove(old_value). A window size of 1000 and 1m values (the size of the SkipList) takes around 1 second or 1000 ns /value.

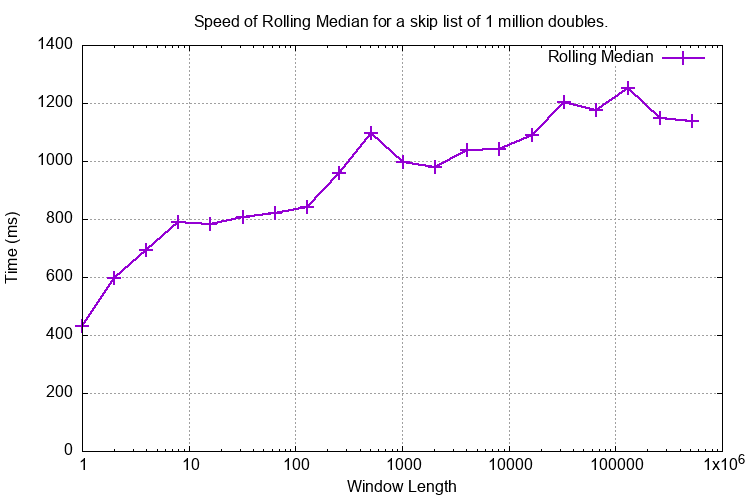
The test function is perf_roll_med_odd_index_wins().

Space Complexity

Space usage is a weakness of SkipLists. There is a large amount of bookkeeping involved with multiple node pointers plus the width values for each node for an indexed SkipList.

Theoretical Memory Usage for double

The space requirements for a SkipList of doubles can be estimated as follows.

t = sizeof(T) ~ typ. 8 bytes for a double. v = sizeof(std::vector<struct NodeRef<T>>) ~ typ. 32 bytes. p = sizeof(Node<T>*) ~ typ. 8 bytes. e = sizeof(struct NodeRef<T>) ~ typ. 8 + p = 16 bytes. Then each node: is t + v bytes.

Linked list at level 0 is e bytes per node and at level 1 is, typically, e / 2 bytes per node (given p() as a fair coin) and so on. So the totality of linked lists is about 2 * e bytes per node.

Then the total is N (t + v + 2 e) which for T as a double is typically 72 bytes per item.

Memory usage can be gauged by any of the following methods:

• Theoretical calculation such as above which gives ~72 bytes per node for doubles.
• Observing a process that creates a SkipList using OS tools, this typically gives ~86 bytes per node for doubles.
• Calling the size_of() method that can make use of its knowledge of the internal structure of a SkipList to estimate memory usage. For double this is shown to be about 76 bytes per node. Any size_of() estimate will be an underestimate if the SkipList <T> uses dynamic memory allocation such as std::string.

Estimate Memory Usage With size_of()

This implementation of a SkipList has a size_of() function that estimates the current memory usage of the SkipList. This function uses sizeof(T) which will not account for any dynamically allocated content, for example if T was a std::string.

Total memory allocation is a function of a number of factors:

• Alignment issues with the members of class Node which has members T _value; and SwappableNodeRefStack<T> _nodeRefs;. If T was a char type then alignment issues on 64 bit machines may mean the char takes eight bytes, not one.
• The size of the SkipLists, very small SkipLists carry the overhead of the HeadNode.
• The coin probability p(). Unfair coins can change the overhead of the additional coarser linked lists. More about this later.

The following graph shows the size_of() a SkipList of doubles of varying lengths with a fair coin. The Y axis is the size_of() divided by the length of the SkipList in bytes per node. Fairly quickly this settles down to around 80 bytes a node or around 10 times the size of a single double. The test name is perf_size_of().

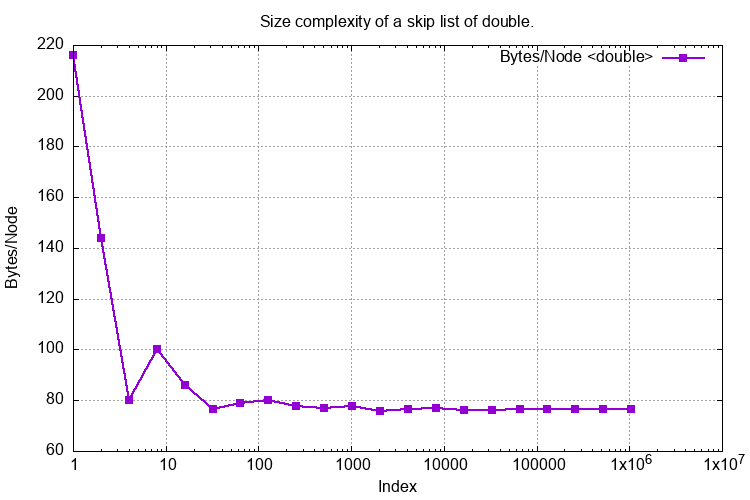
Height Distribution

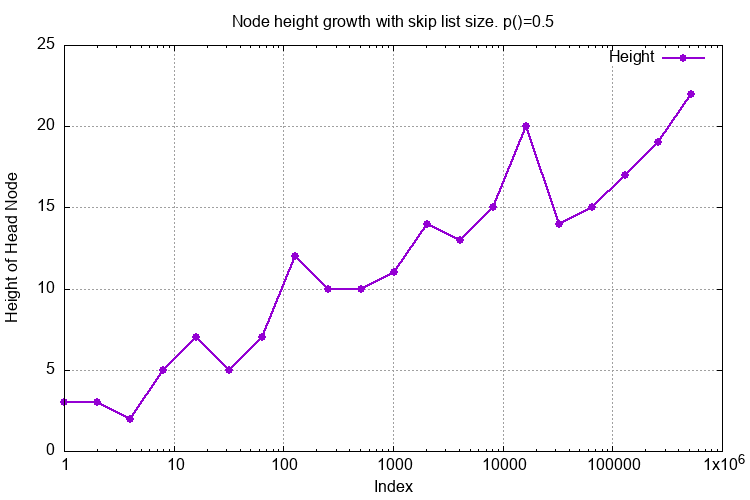
This graph shows the height growth of the SkipList where the height is the number of additional coarse linked lists. It should grow in a log(n) fashion and it does. It is not monotonic as this SkipList is a probabilistic data structure.

Effect of a Biased Coin

The default compilation of the SkipList uses a fair coin. The coin toss is determined by tossCoin() in SkipList.cpp which has the following implementation:

bool tossCoin() {
    return rand() < RAND_MAX / 2;
}

The following biases can be introduced with these return statements:

p()	Return statement
6.25%	return rand() < RAND_MAX / 16;
12.5%	return rand() < RAND_MAX / 8;
25%	return rand() < RAND_MAX / 4;
50%	return rand() < RAND_MAX / 2;
75%	return rand() < RAND_MAX - RAND_MAX / 4;
87.5%	return rand() < RAND_MAX - RAND_MAX / 8;

For visualising what a SkipList looks like with a biased coin see Biased Coin Skip List Visualisations

Time Performance

The following graph plots the time cost of at(middle), has(middle_value), insert(), at(), remove() and the rolling median (window size 101) all on a 1 million long SkipList of doubles against p() the probability of the coin toss being heads. The time cost is normalised to p(0.5).

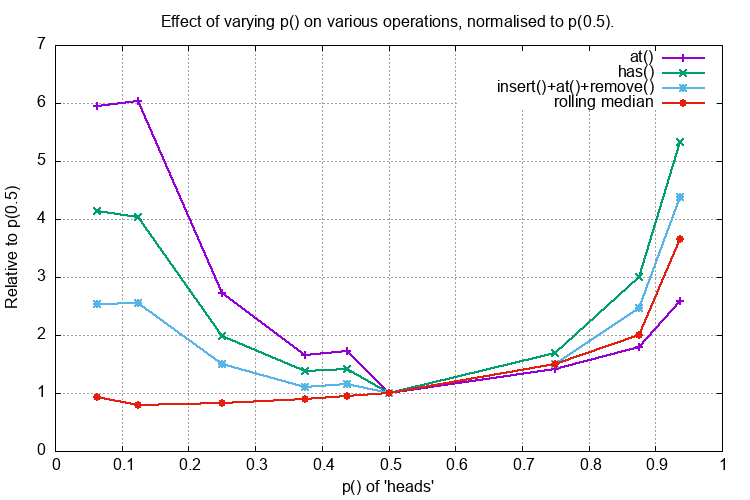
Reducing p() reduces the number of coarser linked lists that help speed up the search so it is expected that the performance would deteriorate. If p() was zero the SkipList would be, effectively, a singly linked list with O(n) search performance. I do not understand why the rolling median performance appears to improve slightly when the rolling median is really just an insert(), at(), remove() operation.

Increasing p() increases the number of coarser linked lists that might be expected to speed up the search. This does not do so in practice, possible explanations are:

• The increased cost of creating a node
• The increased memory usage (see next section)
• Poor locality of reference of the nodes.

Space Performance

Different values of p() greatly influences the space used as it directly affects the number of coarser linked lists created. In practice a reduction of p() provides some small space improvement.

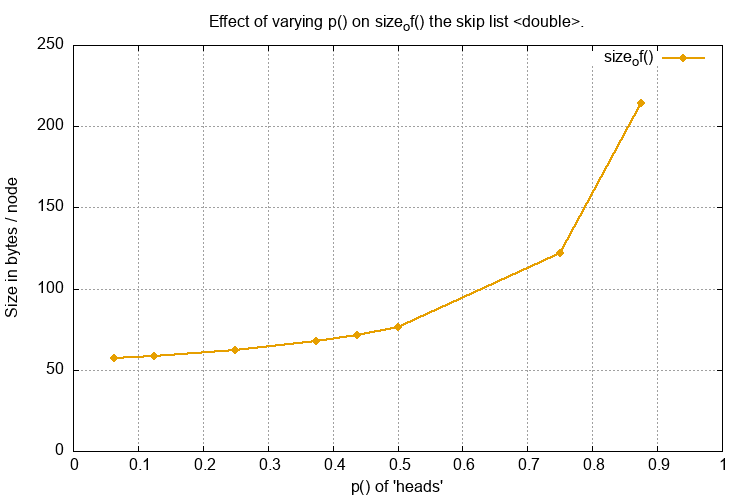
If the SkipList was highly optimised for rolling median operations it might be worth experimenting with p(0.25) or even p(0.125) and evaluate the time/space requirements but otherwise there seems no reason, in the general case, to use anything but p(0.5).

Multi-threaded C++ Performance

The C++ code is capable of multi-threading support where a single SkipList can be mutated by multiple threads. The code must be compiled with the macro SKIPLIST_THREAD_SUPPORT defined.

Test C++ execution code can be run by invoking the the makefile thus:

$ cd src/cpp
$ make release CXXFLAGS=-DSKIPLIST_THREAD_SUPPORT
$ ./SkipList_R.exe
               ...
               test_single_thread_insert(): PASS
       test_two_thread_insert_has_remove(): PASS
      test_two_thread_insert_count_has_remove_count(): PASS
     test_perf_insert_count_has_remove_count_multi_threads_vary_length(): threads:    1 SkiplistSize:   131072 time:       180145 (us) rate       727592 /s
                                            ...
    test_perf_single_thread_fixed_length(): PASS

Final result: PASS
Exec time: x.x (s)
Bye, bye!

Note

If you omit CXXFLAGS=-DSKIPLIST_THREAD_SUPPORT then the threaded tests will be omitted:

$ make release
$ ./SkipList_R.exe
               ...
               test_single_thread_insert(): N/A
       test_two_thread_insert_has_remove(): N/A
      test_two_thread_insert_count_has_remove_count(): N/A

Effect of SKIPLIST_THREAD_SUPPORT

Here are several performance measurements when SKIPLIST_THREAD_SUPPORT is defined:

• A SkipList in a single threaded environment.
• A SkipList in a multi threaded environment where threads vie for the same SkipList.

To explore this we create a task that is to insert a unique double into an empty SkipList 2**14 (16384) times and then remove that number one by one to empty the SkipList. This task typically takes 18 ms (around 1 us per insert+remove).

This task will be repeated 1, 2, 4, … 64 times using single and multiple threads. The single threaded version is sequential, the multithreaded version creates simultaneous operations on the same SkipList.

The code for these tests is in test/test_concurrent.cpp.

A Single Threaded Environment

The sheer act of using -DSKIPLIST_THREAD_SUPPORT will introduce a mutex into the head node. This will increase the time of any operation on the SkipList even when run in the single thread as there is a cost of acquiring the mutex even in the absence of contention. The test function is test_perf_single_thread_fixed_length().

In the graph below the X axis is the number of times the task is repeated (sequentially). The left Y axis is the total execution time with the SkipList in the main thread. The right Y axis is the ratio: time with -DSKIPLIST_THREAD_SUPPORT / time without -DSKIPLIST_THREAD_SUPPORT

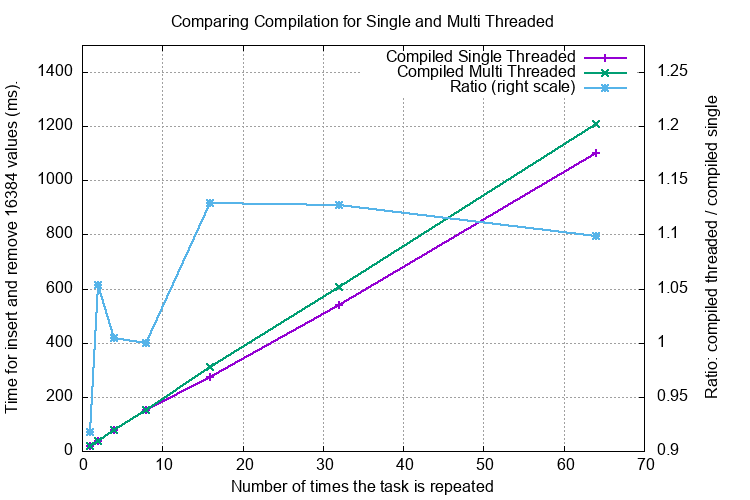
The overhead of using -DSKIPLIST_THREAD_SUPPORT is about 0% to 15%.

A Multi Threaded Environment

Here is a multi-threaded simulation of the operations typical of rolling median on a shared Skip List. Each thread:

• Inserts a value at the mid-point of the same Skip List using insert().
• Checks it has that value using has().
• Removes that value using remove()

Each of these operations obtains a lock on the Skip List.

Then repeating the task in 1, 2, 4, … 128 new threads simultaneously where they share the same Skip List. The test function is _test_perf_sim_rolling_median_multi_thread().

In the graph below the Y-axis shows the cost for each insert/has/remove operation in microseconds against the number of threads contending for the Skip List.

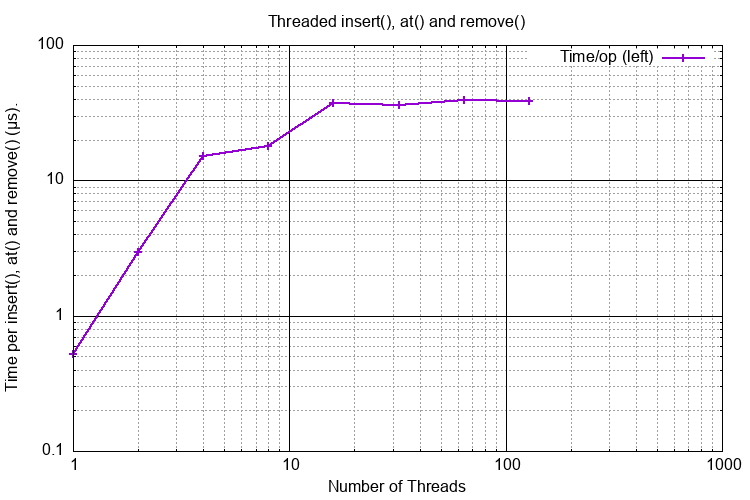
Detailed Performance

The performance test function names all start with perf_... and are as follows. The SkipList type is <double>. In the table below 1M means mega, i.e. 2**20 or 1024*1024 or 1048576:

Test Name	Measure	Time/value	Rate
perf_single_insert_remove()	With an empty SkipList add one item and remove it.	240 ns	4.1 M/s
perf_large_skiplist_ins_only()	Starting with an empty SkipList append 1 million values.	740 ns	1.3 M/s
perf_large_skiplist_ins_rem()	Starting with an empty SkipList append 1 million values then remove the first (lowest) value until the SkipList is empty.	900 ns	1.1 M/s
perf_single_ins_rem_middle()	With a SkipList of 1 million values insert the middle value (i.e. 500,000.0) and remove it.	1200 ns	0.85 M/s
perf_single_at_middle()	With a SkipList of 1 million values find the middle value.	220 ns	4.6 M/s
perf_single_has_middle()	With a SkipList of 1 million values test for the middle value.	210 ns	4.8 M/s
perf_single_ins_at_rem_middle()	With a SkipList of 1 million values call insert(v), at(500000) and remove(v) where v corresponds to the middle value. This simulates the actions of a rolling median.	1400 ns	0.7 M/s
perf_median_sliding_window()	Simulate a rolling median of 100 values. Create an initially empty SkipList. For each of 10,000 random values insert the value into the SkipList. For indicies > 100 extract the middle value from the SkipList as the median then remove the i-100 value from the SkipList.	800 ns	1.3 M/s
perf_1m_median_values()	Simulate a rolling median of 101 values. Similar to perf_median_sliding_window() but uses 1 million values.	720 ns	1.4 M/s
perf_1m_medians_1000_vectors()	Simulate a rolling median of 101 values. Similar to perf_1m_median_values() but uses 1000 values repeated 1000 times.	690 ns	1.4 M/s
perf_simulate_real_use()	Simulate a rolling median of 200 values. Similar to perf_1m_medians_1000_vectors() but uses 8000 values repeated 8000 times i.e. the rolling median of 8000x8000 array.	760 ns	1.3 M/s
perf_roll_med_odd_index()	Tests the time cost of OrderedStructs::RollingMedian::odd_index for 1 million values and a window size of 101.	830 ns	1.2 M/s
perf_index()	Tests the time cost of index() half way through 1m doubles.	200 ns	5 M/s

Time Complexity

There are a number of tests that check the execution time of operations with varying sizes of SkipLists. The expectation is that the time complexity is O(log(n)).

Test Name	Description
perf_at_in_one_million()	For 1M values call at(i) where i ranges from 2**1 to 2**19. This explores the time complexity of at().
perf_has_in_one_million()	For 1M values call has(i) where i ranges from 2**1 to 2**19. This explores the time complexity of has().
perf_roll_med_odd_index_wins()	As perf_roll_med_odd_index() but explores various window sizes from 1 to 524288.
perf_index_vary_length()	For 1M values call index(value) where value ranges from 2**1 to 2**19. This explores the time complexity of index().

Python Performance Tests

Some informal testing of the Python wrapper around the C++ SkipList was done using timeit in tests/perf/test_perf_cSkipList.py. The SkipList has 1m items. The performance is comparable to the C++ tests.

Test	Time per operation (ns)	Factor over C++ time
test_at_integer()	217
test_at_float()	242	x2.7
test_has_integer()	234
test_has_float()	238	x1.4
test_insert_remove_mid_integer()	1312
test_insert_remove_mid_float()	1497	x1.4
test_index_mid_int()	400
test_index_mid_float()	356	x1.9

It is rather surprising, and satisfying, that the Python overhead is so small considering the boxing/unboxing that is going on. The test methodology is different in the Python/C++ cases which might skew the figures.